ब्रह्मांड के ‘सूर्य-केन्द्रिक सिद्धांत’ के प्रणेता
कोपरनिकस नहीं, आर्यभट
 भारतीय इतिहास का गुप्त काल हिंदू धर्म और भारतीय संस्कृति के विकास का युग था। इस युग में भारतीय ज्योतिष अपनी पराकाष्ठा पर थी जिसका श्रेय कई विद्वानों-आर्यभट, वराहमिहिर, भास्कर आदि को जाता है लेकिन आर्यभट प्रथम को भारतीय ज्योतिष का प्रणेता माना जाता है। आर्यभट से पहले भी कई आचार्य हुए हैं जिन्होंने अपने ज्योतिष सिद्धांत-ग्रंथ में अंकगणित, बीजगणित और रेखागणित के प्रश्न दिए हैं। इन ज्योतिषियों में गर्ग की चर्चा कई स्थानों पर आती है। महर्षि गर्ग राजा पृथु के ज्योतिषी थे। गर्ग प्रणीत गार्गीसंहिता अब लुप्तप्राय हो गई है।
भारतीय इतिहास का गुप्त काल हिंदू धर्म और भारतीय संस्कृति के विकास का युग था। इस युग में भारतीय ज्योतिष अपनी पराकाष्ठा पर थी जिसका श्रेय कई विद्वानों-आर्यभट, वराहमिहिर, भास्कर आदि को जाता है लेकिन आर्यभट प्रथम को भारतीय ज्योतिष का प्रणेता माना जाता है। आर्यभट से पहले भी कई आचार्य हुए हैं जिन्होंने अपने ज्योतिष सिद्धांत-ग्रंथ में अंकगणित, बीजगणित और रेखागणित के प्रश्न दिए हैं। इन ज्योतिषियों में गर्ग की चर्चा कई स्थानों पर आती है। महर्षि गर्ग राजा पृथु के ज्योतिषी थे। गर्ग प्रणीत गार्गीसंहिता अब लुप्तप्राय हो गई है।
जब बौद्ध धर्म का ह्रास होने लगा, गुप्तकाल में हिंदू धर्म का उत्थान हुआ और यवनों के ज्योतिष का भी भारत भूमि में आगमन हुआ, तब भारतीय ज्योतिष का भी अध्ययन-अध्यापन जोरों से होने लगा। इसकी परिणति यह हुई कि विक्रम की छठीं शती में ज्योतिष के कई आचार्य हुए, कुछ ने भारतीय ज्योतिष के ग्रंथ रचे, कुछ ने यवन ज्योतिष का सार तैयार किया और कुछ ने दोनों का सार लेकर ज्योतिष के ग्रंथों की रचना की। कुछ विद्वानों ने ज्योतिष के नवोन्मेषों का भी समावेश किया। इनमें सर्वाधिक ख्याति मिली आचार्य आर्यभट प्रथम को और यहीं से भारतीय ज्योतिष की सुसम्बद्ध शृंखला का उत्स भी होता है।
यह कहा जा सकता है कि भारतीय ज्योतिष की जो ध्वजा कीर्ति आचार्य आर्यभट प्रथम के समय (5वीं शती) में फैली, वह भास्कराचार्य के काल तक (12वीं शती) फीकी पड़ चुकी थी। आर्यभट प्रथम और भास्कर द्वितीय प्राचीन भारत के दो महान ध्रुव थे जिनसे ही भारतीय विज्ञान की गौरवशाली परंपरा का उत्स होता है और उन्हीं के साथ समापन भी। इनके बाद विदेशी आक्रांताओं का आवागमन आरंभ हो चुका था। इस काल के बाद जो भी गणितज्ञ हुए, उन्होंने अपने पूर्ववर्ती रचनाकारों की या तो टीकाएं लिखीं अथवा ग्रंथ भी लिखे जो उतने उल्लेखनीय नहीं थे।
आर्यभट प्रथम: प्रख्यात गणितज्ञ एवं ज्योतिर्विद्
प्राचीन भारत में आर्यभट नाम के दो खगोलज्ञ हो चुके हैं। जिन आर्यभट का उल्लेख यहां किया जा रहा है, उनका जन्म कुसुमपुर (पटना) में 476 ई. में हुआ था। चूंकि इसी नाम के एक अन्य खगोलज्ञ लगभग 950 ई. में हुए थे, अतः कुसुमपुर के आर्यभट को आर्यभट प्रथम के नाम से सम्बोधित किया जाता है। इन्होंने अपना जन्मकाल बताते हुए लिखा है कि 60 संवत्सरों के 60 युग और तीन युग पाद (सतयुग, त्र्ोता, द्वापर) जब बीत गए तब मेरे जन्म से 23 वर्ष बीत चुके थे। गणना करने पर यह अवधि ई. सन् 476 ठहरती है।
‘षष्ट्यब्दानां षष्टिर्यदा व्यतीताóयश्च युगपादाः।
त्र्यधिका विंशतिरब्दास्तदेह मय जन्मनोऽतीताः।।1।।
-काल क्रियापाद
 आर्यभट ने 23 वर्ष की अवस्था में 499 ईस्वी में अपने प्रख्यात ग्रंथ ‘आर्यभटीयम्’ की रचना की। आर्यभटीयम् चार खण्डों-गीतिकापाद या दशगीतिका, गणितपाद, कालक्रियापाद और गोलपाद में विभाजित है। गीतिकापाद में 10 श्लोक, गणितपाद में 33 श्लोक, कालक्रियापाद में 25 तथा गोलापाद में 50 श्लोक हैं। आर्यभटीयम् के प्रथम खंड में संख्याओं को अक्षरों द्वारा व्यक्त करने की संकेत लिपि, दूसरे खंड में वर्गमूल, घनमूल निकालने की विधियां, क्षेत्र्ाफल और आयतन निकालने के नियम, वृत्तीय अचर का मूल्य आदि दिए गए हैं। तीसरे खंड में सौर वर्ष, चंद्र मास, नक्षत्र्ा मास, अधिमास, ग्रहों का स्थान निर्धारण तथा चौथे खंड में ध्रुव वृत्त, क्षितिज आदि का वर्णन है।
आर्यभट ने 23 वर्ष की अवस्था में 499 ईस्वी में अपने प्रख्यात ग्रंथ ‘आर्यभटीयम्’ की रचना की। आर्यभटीयम् चार खण्डों-गीतिकापाद या दशगीतिका, गणितपाद, कालक्रियापाद और गोलपाद में विभाजित है। गीतिकापाद में 10 श्लोक, गणितपाद में 33 श्लोक, कालक्रियापाद में 25 तथा गोलापाद में 50 श्लोक हैं। आर्यभटीयम् के प्रथम खंड में संख्याओं को अक्षरों द्वारा व्यक्त करने की संकेत लिपि, दूसरे खंड में वर्गमूल, घनमूल निकालने की विधियां, क्षेत्र्ाफल और आयतन निकालने के नियम, वृत्तीय अचर का मूल्य आदि दिए गए हैं। तीसरे खंड में सौर वर्ष, चंद्र मास, नक्षत्र्ा मास, अधिमास, ग्रहों का स्थान निर्धारण तथा चौथे खंड में ध्रुव वृत्त, क्षितिज आदि का वर्णन है।
गणित में हमारे देश की सबसे युग प्रवर्तक खोज थी दशमलव पद्धति की जो अब सारे विश्व में स्वीकृत हो चली है। यह पहली नौ संख्याओं तथा शून्य पर आधारित है। इस अंक लेखन ने अंक शाóीय गणनाओं एवं पद्धतियों को अत्यंत सरल बना दिया। हिंदू गणितज्ञों में कब और किसने शून्य का आविष्कार किया, ठीक से ज्ञात नहीं है लेकिन इब्नवशिया, अलमसूदी और अलबेरुनी जैसे विद्वान इसके आविष्कार का श्रेय हिंदुओं को देते हैं। शून्य के आविष्कार से पूर्व अंकों के लिए चिह्न हुआ करते थे, जिनके आधार पर कुछ ही गणना की जाती थी, रोमन अंकों की मदद से रोमवासी कुछ हजार तक ही लिख सकते थे। यूनानी भी दस हजार से अधिक न जानते थे। इस बारे में अलबेरुनी (सन् 1031 ईस्वी) ने लिखा है कि अंक क्रम में जो एक हजार से अधिक जानते हैं, वे हिंदू (भारतीय) हैं।
प्राचीन हिंदुओं के पास अंकों को सूचित करने के लिए अंक संज्ञाएं विद्यमान थीं। इस संबंध में आर्यभट अंकों के स्थान का नाम गिनते हुए लिखते हैं - एक (1), दश (10), शत (100), सहस्र (1000), अयुत (10000), नियुत (100000), प्रयुत (1000000), कोटि (10000000), अर्बुद (100000000) और वृंद (1000000000) स्थानों में से प्रत्येक अपने पीछे वाले से दस गुना है।
इतना ही नहीं, आर्यभट ने अंकों के मान के लिए अक्षरों की संकेत लिपि भी बनाई है। संस्कृत वर्णमाला के आधार पर उन्होंने अंक निरूपण की भी प्रणाली दी है।
सूर्य-केंद्रिक सिद्धांत के प्रणेता
 पश्चिम में एक समय ऐसा था जब धर्म एवं अंधविश्वासों ने समाज को बुरी तरह जकड़ रखा था। इन अंधविश्वासी मान्यताओं के विरुद्ध जब विज्ञान ने कुछ कहा तो पुरस्कार स्वरुप वैज्ञानिकों को पोप का कोपभाजन बनना पड़ा। खगोल विज्ञान के इतिहास के प्रारंभिक पृष्ठ कोपरनिकस, ब्रूनो और गैलिलियो के बलिदानों से रक्त रंजित हैं।
पश्चिम में एक समय ऐसा था जब धर्म एवं अंधविश्वासों ने समाज को बुरी तरह जकड़ रखा था। इन अंधविश्वासी मान्यताओं के विरुद्ध जब विज्ञान ने कुछ कहा तो पुरस्कार स्वरुप वैज्ञानिकों को पोप का कोपभाजन बनना पड़ा। खगोल विज्ञान के इतिहास के प्रारंभिक पृष्ठ कोपरनिकस, ब्रूनो और गैलिलियो के बलिदानों से रक्त रंजित हैं।
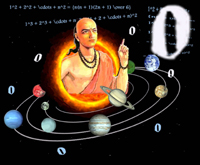
कोपरनिकस (1473-1543) को इस बात का श्रेय है कि उसने ही पहले ब्रह्मांड के ‘सूर्य-केंद्रिक सिद्धांत’ की व्याख्या की। इसका तात्पर्य यह था कि ब्रह्मांडीय गतिविधि का केंद्र सूर्य है न कि पृथ्वी जैसा कि मूर्ख पादरियों और बाइबिल की अवधारणाएं थीं। कोपरनिकस ने 1540 में अपने ग्रंथ ष्क्म त्मअवसनजपवदपइने व्तइपनउ ब्वमसमेजपनउष् में लिखा कि - स ग्रह निकाय का केंद्र पृथ्वी नहीं, वरन् सूर्य है। स सूर्य स्थिर है और पृथ्वी गतिशील है, वह भी अन्य ग्रहों की भांति एक ग्रह है और शुक्र तथा मंगल की कक्षाओं के बीच एक कक्षा में सूर्य की परिक्रमा करती है। यदि हम भारतीय खगोल शास्त्र्ा के पन्नेें पलटें तो हमें पता चलता है कि कोपरनिकस से भी हजार साल पहले भारतीय ज्योतिर्विद् आर्यभट प्रथम (रचनाकाल 499 ई0) ने इस सिद्धांत की व्याख्या की थी। अपने सुप्रसिद्ध ग्रंथ ‘आर्यभटीयम्’ में उन्होंने लिखा कि पृथ्वी अपने अक्ष पर घूमती हुई सूर्य के चारों ओर चक्कर लगाती है। आर्यभट ने यह भी लिखा कि चंद्रमा अथवा अन्य ग्रहों में प्रकाश नहीं है बल्कि वे सूर्य के प्रकाश से प्रकाशित होते हैं तथा पृथ्वी की भांति सूर्य के चारों ओर घूमते हैं। आर्यभट ने सर्वप्रथम पूर्व प्रचलित धारणाओं को निर्मूल करते हुए बताया कि जब हम नाव में गति करते हैं तब सारी स्थिर वस्तुएं उल्टी दिशा में गति करती हुई प्रतीत होती हैं, ठीक इसी प्रकार सूर्य भी पृथ्वी का चक्कर लगाता प्रतीत होता है लेकिन सच तो यह है कि पृथ्वी सूर्य का चक्कर लगाती है। आर्यभट ने बताया कि चंद्र ग्रहण या सूर्य ग्रहण चंद्रमा अथवा सूर्य को राहु के ग्रसने के कारण नहीं बल्कि चंद्रमा पर पृथ्वी की छाया पड़ने से अथवा सूर्य और पृथ्वी के बीच चंद्रमा के आ जाने से होता है। आर्यभट द्वारा निकाली गई वर्ष की अवधि (365ण्2586805 दिन) टालेमी द्वारा स्वीकृति अवधि (365ण्2631579 दिन) की अपेक्षा यथार्थ अवधि (365ण्2563604 दिन) के सन्निकट है। आर्यभट ने 121 श्लोकों वाले ग्रंथ आर्यभटीयम् में न जाने कितनी गूढ़ बातें देकर गागर में सागर को चरितार्थ किया है। आर्यभट द्वितीय, जिन्होंने 950 ई. में ‘महासिद्धांत’ की रचना की थी, का योग उतना महत्वपूर्ण नहीं है। इस ग्रंथ को ‘आर्यसिद्धांत’ भी कहते हैं। आर्यभट द्वितीय की चर्चा हम कालक्रमानुसार आगे करेंगे।
वराहमिहिर: फलित ज्योतिष के प्रणेता
 वराहमिहिर आर्यभट के समकालीन थे। वराहमिहिर किस सन् में उत्पन्न हुए, इसका विवरण हमें नहीं मिलता लेकिन उन्होंने अपने ग्रंथ ‘पंच सिद्धांतिका’ में गणितारंभ वर्ष दिया है अर्थात् जिस वर्ष से उन्होंने अपनी गणनाएं प्रारंभ की और इस आधार पर इनके ग्रंथ का रचनाकाल ईस्वी सन् 505 आता है। वराहमिहिर की मृत्यु के वर्ष का स्पष्ट उल्लेख मिलता है। इनकी मृत्यु 587 ई. में हुई थी, इस प्रकार वराहमिहिर को छठीं शती का ज्योतिषी कहना चाहिए। वराहमिहिर ने गणित ज्योतिष और फलित ज्योतिष (अंधविश्वासों पर आधारित मुहूर्त, योग आदि की विद्या) दोनों पर ग्रंथ रचे हैं। लेकिन इनके गणित ज्योतिष के ग्रंथ ‘पंच सिद्धांतिका’ का अधिक महत्व है। यदि वराह ने यह ग्रंथ न लिखा होता तो आज ज्योतिष शाó का इतिहास अधूरा होता। वास्तव में यह ग्रंथ वराहमिहिर से प्राचीन तथा उनके समकालीन पांच ज्योतिष सिद्धांतों का संग्रह है। आज वे मूल सिद्धांत-ग्रंथ अप्राप्य हैं। पांचों ज्योतिष सिद्धांत - पितामह, वसिष्ठ, रोमक, पौलिश और सूर्य सिद्धांत में से केवल सूर्य सिद्धांत की पांडुलिपि व टीकाएं आज उपलब्ध हैं। अतः वराहमिहिर के इस कृत्य के लिए हमें उनका ऋणी होना चाहिए। वराहमिहिर स्वतंत्र्ा ग्रंथ भी लिख सकते थे लेकिन उन्होंने पुराने सिद्धांतों का संपादन करना अधिक उचित समझा। कदाचित इसीलिए इतिहासकार अलबेरूनी ने वराहमिहिर को अत्यधिक आदर दिया है।
वराहमिहिर आर्यभट के समकालीन थे। वराहमिहिर किस सन् में उत्पन्न हुए, इसका विवरण हमें नहीं मिलता लेकिन उन्होंने अपने ग्रंथ ‘पंच सिद्धांतिका’ में गणितारंभ वर्ष दिया है अर्थात् जिस वर्ष से उन्होंने अपनी गणनाएं प्रारंभ की और इस आधार पर इनके ग्रंथ का रचनाकाल ईस्वी सन् 505 आता है। वराहमिहिर की मृत्यु के वर्ष का स्पष्ट उल्लेख मिलता है। इनकी मृत्यु 587 ई. में हुई थी, इस प्रकार वराहमिहिर को छठीं शती का ज्योतिषी कहना चाहिए। वराहमिहिर ने गणित ज्योतिष और फलित ज्योतिष (अंधविश्वासों पर आधारित मुहूर्त, योग आदि की विद्या) दोनों पर ग्रंथ रचे हैं। लेकिन इनके गणित ज्योतिष के ग्रंथ ‘पंच सिद्धांतिका’ का अधिक महत्व है। यदि वराह ने यह ग्रंथ न लिखा होता तो आज ज्योतिष शाó का इतिहास अधूरा होता। वास्तव में यह ग्रंथ वराहमिहिर से प्राचीन तथा उनके समकालीन पांच ज्योतिष सिद्धांतों का संग्रह है। आज वे मूल सिद्धांत-ग्रंथ अप्राप्य हैं। पांचों ज्योतिष सिद्धांत - पितामह, वसिष्ठ, रोमक, पौलिश और सूर्य सिद्धांत में से केवल सूर्य सिद्धांत की पांडुलिपि व टीकाएं आज उपलब्ध हैं। अतः वराहमिहिर के इस कृत्य के लिए हमें उनका ऋणी होना चाहिए। वराहमिहिर स्वतंत्र्ा ग्रंथ भी लिख सकते थे लेकिन उन्होंने पुराने सिद्धांतों का संपादन करना अधिक उचित समझा। कदाचित इसीलिए इतिहासकार अलबेरूनी ने वराहमिहिर को अत्यधिक आदर दिया है।
‘पंचसिद्धांतिका’ बहुत दिनों तक अप्राप्य थी परंतु प्रोफेसर वूलर ने बड़े श्रम के बाद इसकी दो प्रतियां खोज निकालीं, तत्पश्चात् डॉ. थीबो और पं. सुधाकर द्विवेदी ने 1889 में संस्कृत टीका सहित इसका अंग्रेजी अनुवाद प्रकाशित किया। प्राचीन काल में जिन ग्रंथों में ज्योतिष व गणित शाó की आधारभूत बातें दी जाती थीं, उन्हें सिद्धांत-ग्रंथ कहा जाता था। वराह ने उस समय के प्रचलित पांचों सिद्धांतों को एक साथ कर दिया और यह भी लिखा कि कौन सिद्धांत कैसा है?वराह लिखते हैं - ‘सूर्य सिद्धांत सबसे उत्तम है, उसके बाद रोमक और पौलिश लगभग समकक्ष हैं और शेष दो सिद्धांत इनसे बहुत हीन हैं।’ पंचसिद्धांतिका में इनका विस्तार भी लगभग इसी क्रम में है। पितामह, वसिष्ठ और सौर (सूर्य) सिद्धांत तो अपने यहां के हैं लेकिन रोमक और पौलिश सिद्धांतों के नामों से ही पता लग जाता है कि ये यवन ज्योतिष से संबंधित थे। कुछ विद्वानों का मत है कि वराह ने स्वयं रोम, यूनान आदि पाश्चात्य देशों की यात्र्ाा करके वहां की ज्योतिष का अपनी पंचसिद्धांतिका में समावेश किया लेकिन कुछ का मत यह भी है कि सिकंदर के आक्रमण के बाद ही यूनानी और भारतीय विद्वानों का संपर्क होने लगा था। अतः ज्ञान के आदान-प्रदान के क्रम में यहीं किसी यूनानी विद्वान से उन्हें इनकी जानकारी मिली हो। लेकिन इतना जरूर है कि भारतीय ज्योतिष की ध्वजाकीर्ति चारों ओर फैलने लगी थी। पंचसिद्धांतिका के अतिरिक्त वराह के अन्य ग्रंथ ‘बृहज्जातक’, ‘लघुजातक’, ‘विवाह पटल’ और ‘योग यात्र्ाा’ आदि फलित ज्योतिष के ग्रंथ हैं। वराह की एक और बड़ी पोथी है - ‘‘बृह्त्संहिता’ जो फलित ज्योतिष पर आधारित है। ‘बृहत्संहिता’ में वर्णित ज्योतिष की बातें अब महत्व की नहीं हैं। उसमें ज्योतिष के अतिरिक्त सामाजिक चित्र्ाण, खेती-बाड़ी, राजा-प्रजा की स्थिति आदि का चित्र्ाण है। अन्य ग्रंथ होरा शाó अर्थात् जन्मकुंडली आदि बनाने की विद्या के ग्रंथ हैं।
हम वराहमिहिर के सबसे अधिक ऋणी हैं तो उनकी ‘पंचसिद्धांतिका’ के लिए, जो ज्योतिष शाó के इतिहास का अपूर्व ग्रंथ है। अलबेरूनी ने अपने ग्रंथ ‘भारत वर्ष’ में वराह को अत्यधिक आदर प्रदान करते हुए लिखा है - ‘वराह के कथन सत्य पर आधारित हैं, परमेश्वर करे कि सभी बड़े लोग उसके आदर्श का पालन करें।’ वराहमिहिर के ‘बृहज्जातक’ के एक श्लोक से पता चलता है कि इनके पिता का नाम आदित्यदास था। उन्होंने अपने पिता से ज्ञान भी प्राप्त किया था पर ये इनके ज्योतिष शाó के गुरु नहीं थे। पंचसिद्धांतिका के प्रथमाध्याय की एक आर्ध से स्पष्ट होता है कि इनके गुरु इनके पिता से भिन्न थे। दूसरे स्थलों के कुछ विवरणों से ज्ञात होता है कि वे अवन्ती (उज्जयिनी) के निवासी थे। प्रायः अपने सभी ग्रंथों के आरंभ में मंगलाचरण में इन्होंने सूर्य की वंदना की है जिससे स्पष्ट है कि ये सूर्य के उपासक थे। कायित्थ नामक स्थान में सूर्यदेव को प्रसन्न करके इन्होंने वर प्राप्त किया था। संभवतः यह कपित्थ ग्राम है जो उज्जैन के निकट (आज भी) ‘कायथा’ नाम से विद्यमान है। इनका पुत्र्ा पृथुयश था जिसकी रचना ‘षट्पंचाशिका’ सुप्रसिद्ध है।
ब्रह्मगुप्त: अरबों में भारतीय गणित के प्रसारक
आर्यभट और वराहमिहिर के बाद भारतीय गणितज्ञों एवं ज्योतिषियों में ब्रह्मगुप्त का नाम उल्लेखनीय है। भारत से बाहर सबसे अधिक प्रतिष्ठा इन्हीं को मिली है। कारण स्पष्ट है - अरबों को भारतीय गणित एवं ज्योतिष का ज्ञान सर्वप्रथम ब्रह्मगुप्त के ही ग्रंथों से मिला। अलबेरूनी के आधार पर प्रो. साचो लिखते हैं - ‘प्राच्य सुधार के इतिहास में ब्रह्मगुप्त का स्थान बहुत ऊंचा है। अरबवासियों को टालेमी के ग्रंथ का पता लगने से पूर्व उन्हें ब्रह्मगुप्त ने ज्योतिष शाó सिखाया क्योंकि अरबी भाषा के इतिहास में ‘अल् सिंद हिंद’ और ‘अल अरकंद’ ग्रंथों के नाम बार-बार आते हैं और वे दोनों ब्रह्मगुप्त के ‘बाह्य स्फुट सिद्धांत’ और ‘खंड खाद्यक’ के अनुवाद हैं। ‘खंड खाद्यक’ और ‘ब्राह्म सिद्धांत’ का अलबेरूनी ने अरबी में अनुवाद किया था। बेरूनी सिंध प्रांत में बहुत दिनों तक रहा। उसके लेखों में अनेक स्थलों पर स्पष्ट उल्लेख है जिससे ज्ञात होता है कि उस समय सिंध प्रांत में ब्रह्मगुप्त के ग्रंथों का अधिक प्रचार था। ब्रह्मगुप्त का अनुवाद खलीफा मंसूर के समय में हुआ होगा, ऐसा समझा जाता है। ब्रह्मगुप्त का जन्म 598 ई. में हुआ था। उस समय भिन्नमाल उत्तर गुजरात की राजधानी थी, यह आधुनिक राजस्थान के जालौर जिले में भीनमाल गांव है। इसी स्थान के निवासी थे ब्रह्मगुप्त। उन्होंने 30 वर्ष की वय में (628 ई.) लिखा - ‘ब्राह्म स्फुट सिद्धांत’ और 67 की वय में ‘खंड खाद्यक’ की रचना की। आर्याछंदों में लिखित ‘ब्राह्म स्फुट सिद्धांत’ 24 अध्यायों में है जिसमें दो अध्याय गणित पर हैं और शेष ज्योतिष पर। दोनों अध्यायों में अंकगणित और ज्यामिति के अनेक सूत्र्ा हैं। अंकगणित भाग में ब्रह्मगुप्त ने घनमूल, गणित की चार विधियां, वर्ग, घन, भिन्न अनुपात, त्र्ौराशिक, ब्याज, शून्य, अनंत आदि बहुत से प्रकरण दिए हैं। ब्रह्मगुप्त के काल में हिंदू गणित अपनी पराकाष्ठा पर थी लेकिन तमाम खूबियों के बावजूद ब्रह्मगुप्त में भ्रांतियां देखने को मिलती हैं। ब्रह्मगुप्त का यह लिखना कि शून्य को शून्य से भाग देने पर परिणाम शून्य होता है, भ्रामक है। हम भलीभांति जानते हैं कि परिणाम कुछ भी (अनिर्धार्य) हो सकता है। इसी प्रकार वृत्त की परिधि और व्यास के अनुपात के बारे में ब्रह्मगुप्त गलत थे। उन्होंने इस अनुपात का मूल्य 10 बताया है। आर्यभट ने इसी अनुपात के लिए इससे सूक्ष्म मान दिया था। आगे चलकर वृद्धावस्था में ब्रह्मगुप्त ने ‘खंड-खाद्यक’ नामक एक करण ग्रंथ की रचना की जिससे तिथि, नक्षत्र्ा और ग्रहों की गणना सुगम रीति से की जा सके। यह ग्रंथ पंचांग बनाने की विधियों पर प्रकाश डालता है। आश्चर्य की बात है कि जिस ब्रह्मगुप्त ने ‘बाह्यस्फुट सिद्धांत’ में आर्यभट की अनेक स्थलों पर निंदा की थी, उसी ने अपने इस ग्रंथ को आर्यभट के अनुसार बनाया और आरंभ में लिखा - ‘आर्यभट के समान फल देने वाला ग्रंथ बना रहा हूं।’ प्रकट है कि इन्हें वृद्धावस्था में आर्यभट का महत्व प्रतीत हुआ।
आर्यभट द्वितीय: महासिद्धांत के प्रणेता
पांचवी शती के उद्भट गणितज्ञ एवं प्रख्यात खगोलज्ञ आर्यभट की चर्चा आरंभ में की जा चुकी है, चूंकि, आगे चलकर 10वीं शती में, इसी नाम के एक और ज्योतिर्विद् हुए हैं, अतः इन्हें हम ‘आर्यभट द्वितीय’ नाम से संबोधित करेंगे।
आर्यभट द्वितीय ने सिद्धांत ग्रंथ की रचना लगभग 950 ई. में की थी, जिसे ‘महासिद्धांत’ अथवा ‘आर्यसिद्धांत’ नाम से जाना जाता है। आर्यभट प्रथम ने ‘आर्यभटीयम्’ नामक जो अपना ग्रंथ रचा था, उसे भी कुछ समीक्षक ‘आर्यसिद्धांत’ नाम से विहित करते हैं, जो भ्रमकारक है।
यद्यपि इन्होंने कहीं भी अपने काल का उल्लेख नहीं किया है लेकिन डॉ. विभूति भूषण दत्त, डॉ. अवधेश नारायण सिंह और शंकर बाल कृष्ण दीक्षित प्रभृति विद्वानों का मत है कि इनका काल शक 872 के आस-पास का है जो कि ईस्वी सन् 950 आता है। इसी नाते इन्हें आर्यभट द्वितीय नाम से जाना जाता है।
आर्यभट द्वितीय प्रणीत ‘महासिद्धांत’ में 18 अधिकार और प्रायः 625 आर्या छंद हैं। प्रारंभिक 13 अध्याय वे ही हैं जो कि ‘सूर्यसिद्धांत’ और ‘ब्राह्मस्फुट सिद्धांत’ में वर्णित अध्याय हैं, मात्र्ा दूसरे अध्याय का नाम ‘पराशर मताध्याय’ रखा गया है। 14वां अध्याय ‘गोलाध्याय’ है। इसके प्रथम 11 श्लोकों तक पाटी गणित (अंकगणित) के प्रश्न दिए गए हैं और 3 श्लोक भूगोल के प्रश्नों पर आधारित हैं तथा शेष 43 श्लोकों में अहर्गण और ग्रहों की मध्यम गति संबंधी प्रश्न दिए गए हैं। 15वें अध्याय में पाटी गणित, क्षेत्र्ाफल, घनफल आदि विषयक 120 आर्याएं दी हुई हैं। 16वां अध्याय ‘भुवनकोश-प्रश्नोत्तर’ है, जिसमें भूगोल, खगोल, स्वर्गादि लोक वर्णित हैं। 17वें अध्याय का नाम ‘प्रश्नोत्तर अध्याय’ रखा गया है, जिसके वर्ण्य विषय ग्रहों की मध्य गति संबंधी प्रश्न आदि हैं। 18वां और अंतिम अध्याय कुट्टकाध्याय है। इसमें ‘कुट्टक’ ;च्नसअतपेमतद्ध संबंधी प्रश्न ब्रह्मगुप्त प्रणीत ‘ब्राह्म-स्फुट सिद्धांत’ की अपेक्षा कहीं अधिक सुविचारित हैं।
आर्यभट द्वितीय ने अंक लेखन की नई पद्धति अपने ग्रंथ में अपनाई है जो कि आर्यभट की पद्धति से भिन्न है। वर्णों के माध्यम से संख्याओं को प्रकट करने में आर्यभट प्रथम ने ‘अंकानाम् वामतो गतिः’ का अनुपालन किया है अर्थात् अंक दाहिनी ओर से बायीं ओर को लिखे जाते हैं लेकिन आर्यभट द्वितीय की पद्धति में संख्याएं सदा बायीं ओर से दाहिने ओर लिखी जाती हैं।
आर्यभट द्वितीय आविष्कृत नवीन अंक लेखन पद्धति ‘क ट प या दि’ पद्धति कहलाती है क्योंकि इसमें 1 के लिए क, ट, प, य अक्षर प्रयुक्त होते हैं। इसी तरह 2 के लिए ख, ठ, फ, र आदि। शून्य के लिए ञ और न प्रयुक्त किए जाते हैं। यथा:
क, ट, प, य त्र 1
ख, ठ, फ, र त्र 2
ग, ड, ब, ल त्र 3
घ, ढ, भ, व त्र 4
ङ, ण म, श त्र 5
च, त, ष त्र 6
छ, थ, स त्र 7
ज, द, त्र 8
झ, ध, त्र 9
ञ, न, त्र 0
इस पद्धति में संख्या लिखने के लिए अक्षरों को क्रमशः बायें से दाहिने ओर लिखते हैं, जैसे कि अंकों से संख्याएं प्रकट की जाती हैं। उदाहरण के लिए घ ड फ का तात्पर्य 432 से है। इसी तरह ज द प का अर्थ 881 से है।
स्वर और उनकी मात्र्ााओं का इस पद्धति में कोई मूल्य नहीं है। मात्र्ााओं के जोड़ने से भी अक्षर वही अर्थबोध देते हैं जैसा कि बिना मात्र्ााओं के। मात्र्ााएं केवल उच्चारण की सुविधा के लिए जोड़ी जाती है। उदाहरणार्थ क, का, कि, कू आदि सभी से 1 का ही अर्थबोध होता है।
इस पद्धति के अनुसार यदि हम आर्यभट प्रथम के उदाहरणों में से एक कल्प में सूर्य और चंद्रमा के भगण लिखें तो उनकी संख्या निम्नवत होगी। यथा:
1 कल्प में सूर्य के भगण घडफेननेनननुनीना
4320000000
1 कल्प में चंद्र के भगण मथथमगग्लभननुना
57753334000
कहना न होगा कि अंक लेखन की यह पद्धति आर्यभट प्रथम की रीति से कहीं सुगम है और स्मरण करने में भी सरल प्रतीत होती हैं। लेखन और स्मरण दोनों दृष्टियों से यह पद्धति सरल है।
sdprasad24oct@yahoo.com